行测备考：利用特值法速解工程问题

【考试咨询】全国公考交流群（日更课）：825845872｜微信公众号：展鸿教育｜官老师：18969902976

公务员招考公告｜历年真题｜32学苑免费课程｜面授班级

行测数量关系中工程问题是热门题型之一，其中又以多者合作尤为常考，多者合作指一项工程是由两个或两个以上对象合作完成，解决该类问题的关键点在于梳理合作时的工作情况，一般情况下我们会结合工程问题的基本公式构建方程。除此之外，我们也常常使用特值解决多者合问题，接下来带大家一起来看几种在工程问题中常用的设特值的方法：

一、将各主体完工天数的最小公倍数设为工作总量

【例1】一批零件若交由赵师傅单独加工，需要10天完成；若交由孙师傅单独加工，需要15天完成。两位师傅一起加工这些零件，需要（    ）天完成。

A.5 B.6 C.7 D.8

【答案】B。解析：设零件总数为30，则赵师傅每天完成3，孙师傅每天完成2，两人一起加工需要30÷（3+2）=6天完成，故本题选B。

二、将各主体的效率比直接设为效率

【例2】甲、乙、丙三人共同完成一项工作需要6小时。如果甲与乙的效率比为1:2，乙与丙的效率比为3:4，则乙单独完成这项工作需要多少小时？（    ）

A.10 B.17 C.24 D.31

【答案】B。解析：由题可知，甲、乙、丙的工作效率之比为3:6:8，则可设甲、乙、丙的工作效率分别为3、6、8，故总工作量为（3+6+8）×6，因此乙单独完成这项工作需要（3+6+8）×6÷6=17小时。故本题选B。

三、多个主体合作，且每个主体的工作效率一样时，设每个主体的工作效率为1

【例3】某茶园需要在一定时间内完成采摘。前4天安排了20名采茶工，完成了五分之一的工作量。如果再用10天完成全部采摘，至少还需要增加（    ）名采茶工。

A.12 B.11 C.10 D.9

【答案】A。解析：设一名采茶工一天的工作量为1，则前4天20名采茶工完成的工作量为4x20=80，占工作量的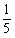，则采摘茶叶的工作总量为80÷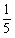=400，此时剩余工作量为400-80=320，若在10天完成，则需要320÷10=32名采茶工，因此至少还需要增加32-20=12名采茶工。故本题选A。